Q cell analysis

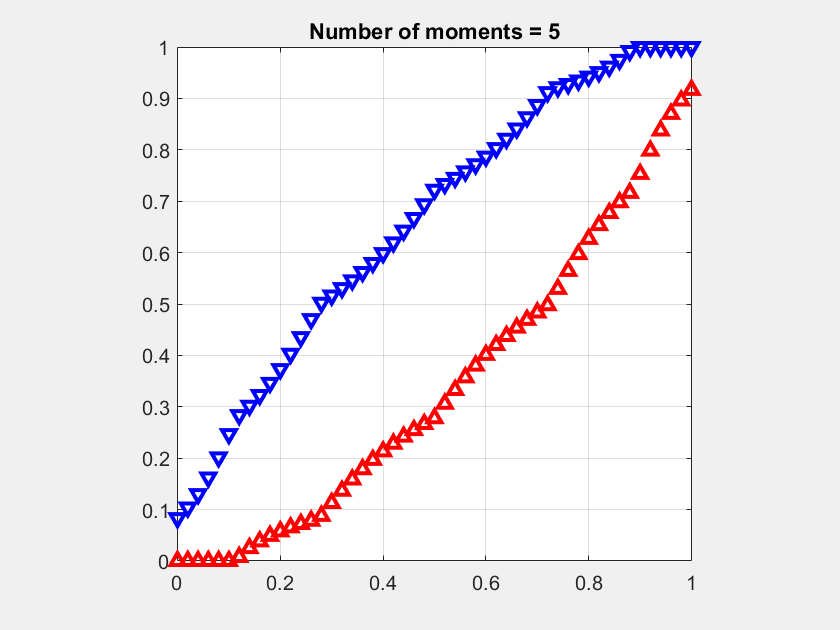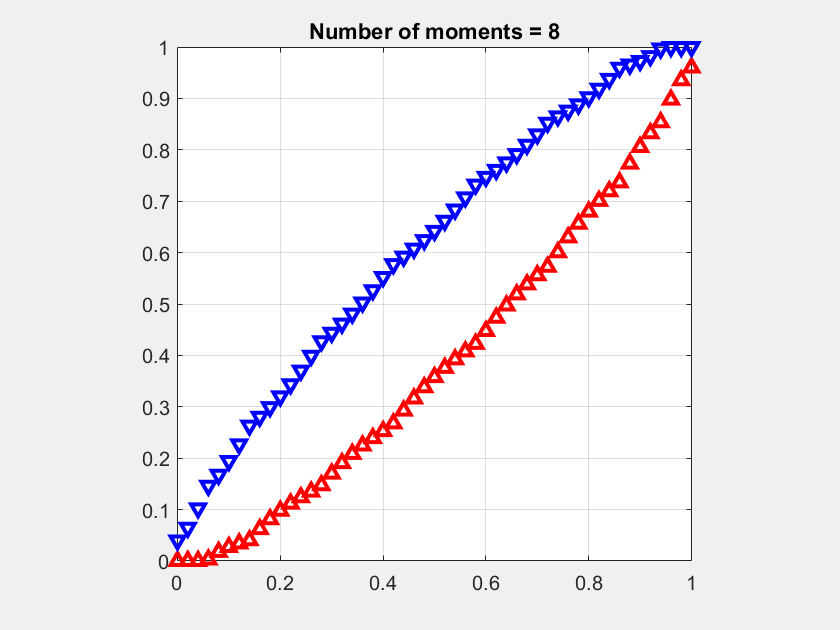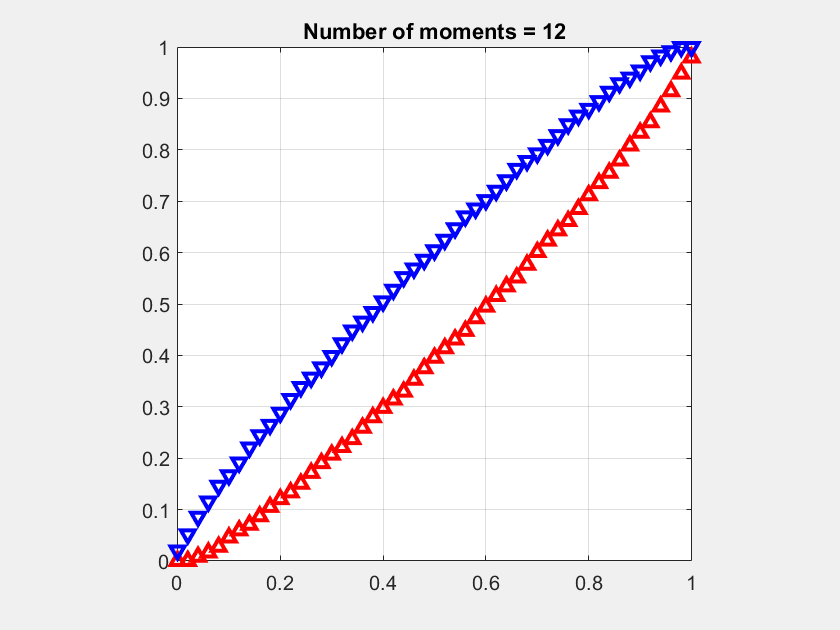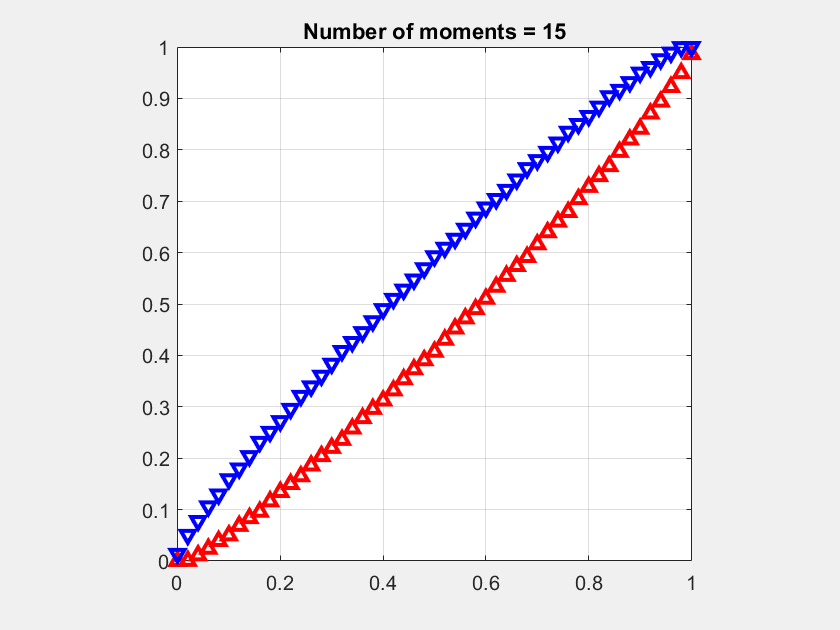
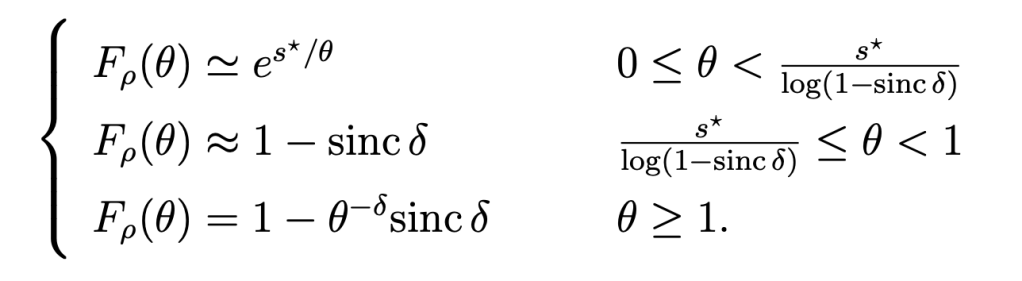Coverage is a key metric in wireless networks but usually only analyzed in terms of the covered area fraction, which is a scalar in [0,1]. Here we discuss a method to analytically bound the coverage manifold 𝒞, formed by the locations y on the plane where users are covered in the sense that the probability that the signal-to-interference ratio (SIR) exceeds a threshold θ is at least u (as argued here, this is a sensible definition of coverage):

$\displaystyle\mathcal{C}\triangleq\{y\in\mathbb{R}^2\colon \mathbb{P}(\text{SIR}(y)>\theta)>u\}.$

SIR(y) is the SIR measured at y for a given set of transmitters 𝒳={x₁,x₂,…} where the nearest transmitter provides the desired signal while all others interfere. It is given by

$\displaystyle\text{SIR}(y)=\frac{h_1r_1^{-\alpha}}{\sum_{i>1}h_ir_i^{-\alpha}}=\frac{1}{\sum_{i>1}\frac{1}{H_i}\left(\frac{r_1}{r_i}\right)^{\alpha}},$

where r_i is the distance to the i-th nearest transmitter to y and the coefficients H_i=h₁/h_i are identically distributed with cdf F_H. The coverage cell when x is the desired transmitter is denoted as C_x, so 𝒞 is the union of all C_x, x∈𝒳. To find an outer bound to the C_x, we are defining a cell consisting of locations at which there is no single interferer that causes them to be uncovered. In that cell, which we call the Q cell Q_x, the ratio of the distance to the nearest interferer to the distance of the serving transmitter has to be larger than a suitably chosen parameter ρ, i.e.,

$\displaystyle Q_x(\rho)\triangleq\left\{y\in\mathbb{R}^2\colon \frac{\|\mathcal{X}\setminus\{x\}-y\|}{\|x-y\|}>\rho\right\}.$

The numerator is the distance to the nearest interferer to y. The shape of the Q cell is governed by a first key insight (which is 2200 years old):
Key Insight 1: Given two points, the locations where the ratio of the distances to the two points equals ρ form a circle whose center and radius depend on the two points and ρ.
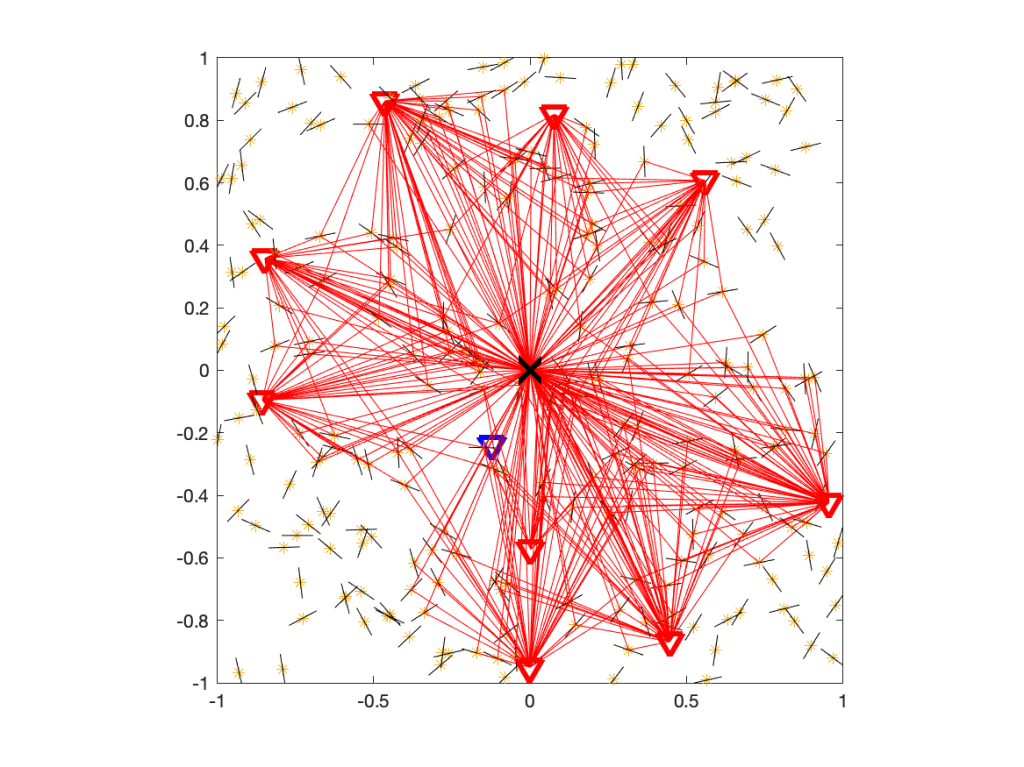
For ρ>1, which is the regime of practical interest, the Q cell is the intersection of a number of disks, one for each interferer. For the more distant interferers, the radii of the disks get large that they are not restricting the Q cell. As a result, a Q cell consists of either just one disk, the intersection of two disks, or a polygon plus a small number of disk segments. In the example in Figure 1, only the four disks with black boundaries are relevant. Their centers and radii are given by the locations of the four strongest interferers, marked by red crosses.

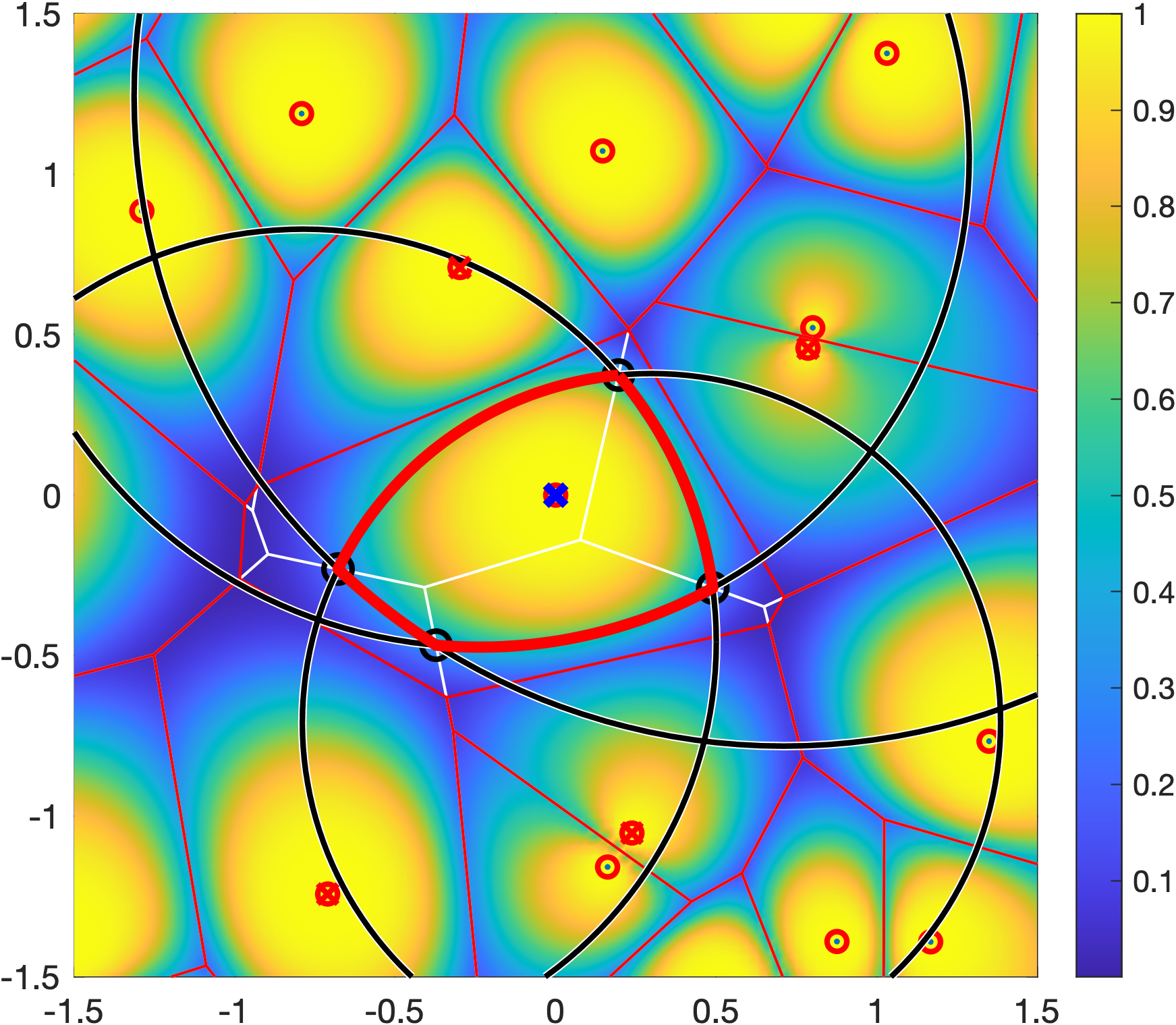
Fig. 1. *The boundary of the Q cell for ρ*=`√`2 *of the transmitter at the origin is shown in red. It is formed by four black circles.* The square is colored according to ℙ(SIR>1) for Rayleigh fading.

The remaining question is the connection between the distance ratio parameter ρ and the quality-of-service (QoS) parameters θ and u. It is given as

$\displaystyle \rho=\sigma(\theta,u)^{1/\alpha},$

where

$\displaystyle \sigma(\theta,u)\triangleq\frac{\theta}{F_H^{-1}(1-u)}$

is called the stringency and F_H^-1 is the quantile function of H (inverse of F_H). For Rayleigh fading,

$\displaystyle \sigma(\theta,u)=\theta\frac{u}{1-u}.$

Figure 1 shows a Q cell for θ=1 and u=0.8, hence (with Rayleigh fading) ρ^α=4, and ρ=√2 for α=4. It is apparent from the coloring that outside the Q cell, the reliability is strictly smaller than 0.8.
The second key important insight is that the Q cells only depend on ρ, so there is no need to explore the three-dimensional parameter space (θ, u, α) in analysis or visualization.
Key Insight 2: The Q cells are the same for all combinations of θ, u, and α that have the same ρ.
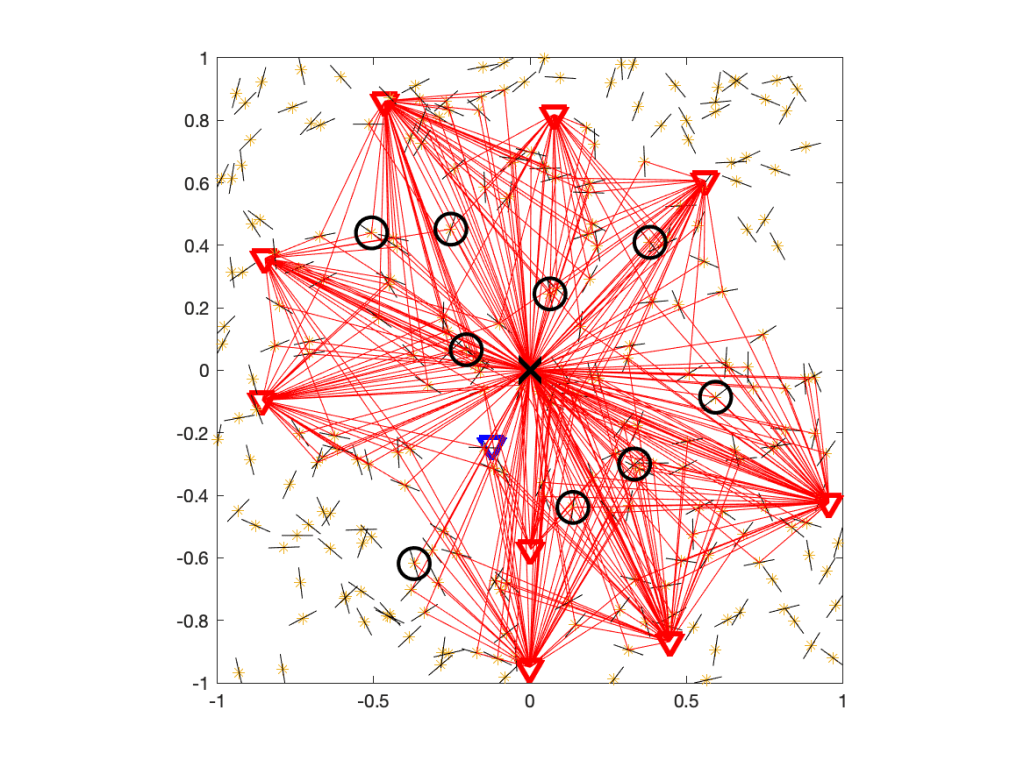
Accordingly, Figure 2, which shows Q cells for four values of ρ, encapsulates many combinations of θ, u, and α.

Fig. 2. *Q cells for ρ=1.25, 1.50, 2.00, 2.50 for 25 transmitters.*

If ρ=1, the Q cells equal the Voronoi cells, and for ρ<1, they span the entire plane minus an exclusion disk for each interferer. This case is less relevant in practice since it corresponds to very lax QoS requirements (small rate and/or low reliability, resulting in a stringency less than 1).

Since C_x ⊂ Q_x for each transmitter x, the union of Q cells is an outer bound to the coverage manifold.

If 𝒳 is a stationary and ergodic point process, the area fraction of the coverage manifold corresponds to the meta distribution (MD) of the SIR, and the area fraction covered by the Q cells is an upper bound to the MD. For the Poisson point process (PPP), the Q cells cover an area fraction of ρ^-2, and for any stationary point process of transmitters, they cover less than 4/(1+ρ)². This implies that for any stationary point process of users, at least a fraction 1-4/(1+ρ)² of users is uncovered. This shows how quickly users become uncovered if the stringency increases.

Details on the calculation of the stringency for different fading models and the proofs of the properties of the Q cells can be found here. This paper also shows a method to refine the Q cells by “cutting corners”, which is possible since the corners of the Q cells have two interferers are equal distance but only one is taken into account. Further, if the MD is known, the refined Q cells can be shrunk so that their covered area fraction matches the MD; this way, accurate estimates of the coverage manifolds are obtained. Figure 3 shows an example of refined and scaled refined Q cells where the transmitters form a perturbed (noisy) square lattice, in comparison with the exact coverage cells C_x.

Fig. 3. *Refined Q cells (blue) and estimated coverage cells (yellow) for ρ=√2. The boundaries of the exact coverage cells are shown in red.*

Due to the simple geometric construction, bounding property, and general applicability to all fading and path loss models, Q cell analysis is useful for rapid yet accurate explorations of base station placements, resource allocation schemes, and advanced transmission techniques including base station cooperation (CoMP) and non-orthogonal multiple access (NOMA).

Is the IRS interfering?

There is considerable interest in wireless networks equipped with intelligent reflecting surfaces (IRSs), aka reconfigurable intelligent surfaces or smart reflecting surfaces. While everyone agrees that IRSs can enhance the signal over a desired link, there are conflicting views about whether IRSs matched to a certain receiver causes interference at other receivers. The purpose of this blog is to clarify this point.

To this end, we focus on a downlink cellular setting where BSs form a stationary point process Φ and a user and a passive IRS with N elements are placed in each (Voronoi) cell. The exact distribution is irrelevant for our purposes. The desired signal at each user consists of the direct signal from its BS plus the intelligently reflected signal at its IRS. The SIR of a user at the origin served by the BS at x₀ can be expressed as

$\displaystyle \text{SIR}=\frac{G \ell(x_0)}{I},$

where ℓ(x₀) is the path loss from the serving BS and

$\displaystyle G=\Big|g_0+\sqrt{\Delta}\sum_{i=1}^N g_{i,1}g_{i,2}\Big|^2.$

Here the random variables g₀ and g_i capture the (amplitude) fading over the direct link and reflected (indirect) link respectively, and the triangle parameter Δ captures the distances in the BS-IRS-user triangle. For details, please see this paper. The pertinent question is what constitutes the interference I. If all BSs are active, their interference is

$\displaystyle I_{\rm BS}=\sum_{x\in\Phi\setminus\{x_0\}} |g_x|^2\ell(x).$

But how about the IRSs? This is where it becomes contentious. Some argue that the IRSs emit signals and thus cause extra interference that is not captured in this sum over the BSs only. This would mean that we need to add a sum over the IRSs of the form

$\displaystyle Q=\sum_{z\in\Psi\setminus\{z_0\}} p_z |g_z|^2\ell(z),$

where Ψ is the point process of IRSs and p_z is the power emitted by the IRS located at z. To decide whether Q is real or fake, let us have a look at the underlying network model. With fading modeled as Rayleigh, it is understood that the propagation of all signals is subject to rich scattering, i.e., there is multi-path propagation. For the case without IRSs, the propagation of interfering signals is illustrated here:

Figure 1. *Propagation in a rich scattering environment without IRSs.*

Figure 1 shows the user at the origin, its serving BS (blue triangle), and the interfering BSs (red triangles). The small black lines indicate scattering and reflecting objects. Some of the paths from interfering BSs via scattering objects to the user are shown with 319 red lines.

Now, let’s add one IRS per interfering BS. The resulting propagation environment is shown in Figure 2.

Figure 2. *Propagation in a rich scattering environment with IRSs.*

From the perspective of the user at the origin, the IRSs are unmatched, which means they act just like any of the other scattering and reflecting objects. So the difference to the IRS-free case is that there is a tiny fraction of additional scatterers, as highlighted in Figure 3.

Figure 3. *Same as Figure 2, but with the IRSs encircled.*

In this case, the IRSs add 4% to the scattering objects. If we did raytracing, they could make a small difference. In analytical work where the fading model is based on the assumption of a large number of scatterers, with the number of propagation paths tending to infinity, they make no difference at all. So we conclude that there is no extra interference Q due to the presence of passive IRSs and thus I=I_BS. The signals reflected at unmatched IRSs are no different from signals reflected at any other object, and multi-path fading models already incorporate all such reflections.

Another argument that IRSs cannot cause extra interference is based on the fundamental principle of energy conservation. If Q did exist, its mean would be proportional to the density of IRSs deployed. This implies that there would be a density of IRSs beyond which the “interference” from the IRSs exceeds the total power transmitted by all BSs, which obviously is not physically possible.

Taming the meta distribution

The derivation of meta distributions is mostly based on the calculation of the moments of the underlying conditional distribution. The reason is that except for highly simplistic scenarios, a direct calculation is elusive. Recall the definition of a meta distribution

$\displaystyle\bar F(t,x)=\mathbb{P}(P_t>x),\qquad\text{\sf where }\;\;P_t=\mathbb{P}(X>t\mid\Phi).$

Here X is the random variable we are interested in, and Φ is part of the random elements X depends on, usually a point process modeling the locations of wireless transceivers. The random variable P_t is a conditional distribution given Φ.

Using stochastic geometry, we can often derive moments of P_t. Since P_t has finite support, finding its distribution given the moments is a Hausdorff moment problem, which has a rich history in the mathematical literature but is not fully solved. The infinite sequence of integer moments uniquely defines the distribution, but in practice we are always restricted to a finite sequence, often less than 10 moments or so. This truncated version of the problem has infinitely many solutions, and the methods proposed to find or approximate the solution to the standard problem may or may not produce one of the solutions to the truncated one. In fact, they may not even provide an actual cumulative distribution function (cdf). On overview of the existing methods and some improvements can be found here.

In this blog, we focus on a method to find the infimum and supremum of the infinitely many possible cdfs that have a given finite moment sequence. The method is based on the Chebyshev-Markov inequalities. As the name suggests, it generalizes the well-known Markov and Chebyshev inequalities, which are based on moments sequences of length 1 or 2. The key step in this method is to find the maximum probability mass that can be concentrated at a point of interest, say z. This probability mass corresponds to the difference between the infimum and the supremum of the cdf at z. This technical report provides the details of the calculation.

Fig. 1 shows an example for the moment sequence m_k =1/(k+1), for k ∈ [n], where the number n of given moments increases from 5 to 15. It can be observed how the infimum (red) and supremum (blue) curves approach each other as more moments are considered. For n → ∞, both would converge to the cdf of the uniform distribution on [0,1], i.e., F(x)=x. The supremum curve lower bounds the complementary cdf. For example, for n =15, ℙ(X>1/2)>0.4. This is the best bound that can be given since this value is achieved by a discrete distribution.

Fig. 1. Infima (red) and suprema (blue) of all the cdfs corresponding to the truncated moment problem where 5 to 15 moments are given.

The average of the infimum and supremum at each point naturally lends itself as an approximation of the meta distribution. It can be expected to be significantly more accurate than the usual beta approximation, which is based only on the first two moments.

An implementation is available in GitHub at https://github.com/ewa-haenggi/meta-distribution/blob/main/CMBounds.m.

Acknowledgment: I would like to thank my student Xinyun Wang for writing the Matlab code for the CM inequalities and providing the figure above.

How well do distributions match? A case for the MH distance

Papers on wireless networks frequently present analytical approximations of distributions. The reference (exact) distributions are obtained either by simulation or by the numerical evaluation of a much more complicated analytical expression. The approximation and the reference distributions are then plotted, and a “highly accurate” or “extremely precise” match is usually declared. There are several issues with this approach.
First, people disagree on what “highly accurate” means. If there is a yawning gap between the distributions, can (should) the match be declared “very precise”? Without any quantification of what “accurate” or “precise” means, it is hard to argue one way or another.
Second, the visual impression can be distorted due to the use of a logarithmic (dB) scale and since, if the distribution has infinite support, only part of it can ever be plotted.

In this post I suggest an approach that addresses both these issues, assuming that at least one of the distributions in question is only available in numerical form (discrete data points). For the second one, we use the Möbius homeomorphic transform to map the infinite support to the [0,1] unit interval. Focusing on complementary cumulative distributions (ccdfs) and assuming the original distribution is supported on the positive real line, the mapped ccdf is obtained by

${ \bar{F}_{\rm MH}(t)=\bar F\left(\frac{t}{1-t}\right).}$

The MH transform and its advantages are discussed in this blog. For instance, it is very useful when applied to SIR distributions. In this case, the mapped ccdf is that of the signal fraction (ratio of desired signal power to total received power). For our purposes here, the [0,1] support is key as it allows not only a complete visualization but also lends itself as a natural distance metric that is itself normalized to [0,1]. Here is the definition of the MH distance:

${\rm d}_{\rm MH}(\bar F,\bar G)\triangleq \|\bar F_{\rm MH}-\bar G_{\rm MH}\|_{\ell_1}=\int_0^1 \big|\bar F\left(\frac{t}{1-t}\right)-\bar G\left(\frac{t}{1-t}\right)\big|{\rm d}t$

Trivially it is bounded by 1, so the distance value directly and unambiguously measures the match between the ccdfs. Accordingly, we can use terms such as “mediocre match” or “good match” depending on this distance. The terminology should be consistent with the visual impression. For instance, if the MH ccdfs are indistinguishable, the match should be called “perfect”. Therefore, to address the first issue raised above, I propose the following intervals and terms.

term for match	range
bad	0.05 – 1
mediocre	0.02 – 0.05
acceptable	0.01 – 0.02
good	0.005 – 0.01
excellent	0.002 – 0.005
perfect	0 – 0.002

Table: Proposed terminology for match based on MH distance.

Another advantage of the MH distance is that it emphasizes the high-value regime (the ccdf near 0) over the low-value regime since it maps values near 0 without distortion while it compresses high values. In the case of SIR ccdfs whose value indicate reliabilities, high values mean high reliabilities, which is the relevant regime in practice.
A simple Matlab implementation of the MH distance is available here. It accepts arbitrary values of the ccdf’s arguments and uses interpolation to achieve uniform sampling of the [0,1] interval.

As an example, here is an animation showing a standard exponential ccdf (MH mapped of course) in blue and another exponential ccdf with a parameter varying from 1.5 to 0.64. It is apparent that the terminology corresponds to the visual appraisal of the gap between the two ccdfs.

*Figure: Illustration of MH distance and corresponding quality of the match between two exponential ccdfs.*

Meta visualization

In this post we contrast the meta distribution of the SIR with the standard SIR distribution. The model is the standard downlink Poisson cellular network with Rayleigh fading and path loss exponent 4. The base station density is 1, and the users form a square lattice of density 5. Hence there are 5 users per cell on average.

Fig. 1: *The setup. Base stations are red crosses, and users are blue circles. They are served by the nearest base station. Cell boundaries are dashed.*

We assume the base stations transmit to the users in their cell at a rate such that the messages can be decoded if an SIR of θ =-3 dB is achieved. If the user succeeds in decoding, it is marked with a green square, otherwise red. We let this process run over many time slots, as shown next.

Fig. 2: *Transmission success (green) and failure (red) at each user over 100 time slots.*

The SIR meta distribution captures the per-user statistics, obtained by averaging over the fading, i.e., over time. In the next figure, the per-user reliabilities are illustrated using a color map from pure red (0% success) to pure green (100% success).

Fig. 3: *Per-user reliabilities, obtained by averaging over fading. These are captured by the SIR meta distribution*. Near the top left is a user that almost never succeeds since it is equidistant to three base stations.

The SIR meta distribution provides the fractions of users that are above (or below) a certain reliability threshold. For instance, the fraction of users that are at least dark green in the above figure.

In contrast, the standard SIR distribution, sometimes misleadingly called “coverage probability”, is just a single number, namely the average reliability, which is close to 70% in this scenario (see, e.g., Eqn. (1) in this post). Since it is obtained by averaging concurrently over fading and point process, the underlying network structure is lost, and the only information obtained is the average of the colors in Fig. 3:

Fig. 4: *The standard SIR distribution only reveals the overall reliability of 70%.*

The 70% reliability is that of the typical user (or typical location), which does not correspond to any user in our network realization. Instead, it is an abstract user whose statistics correspond to the average of all users.

Acknowledgment: The help of my Ph.D. student Xinyun Wang in writing the Matlab program for this post is greatly appreciated.

Realistic communication

Today’s blog is about realistic communication, i.e., what kind of performance can realistically be expected of a wireless network. To get started, let’s have a look at an excerpt from a recent workshop description:

“Future wireless networks will have to support many innovative vertical services, each with its own specific requirements, e.g.

End-to-end latency of 1 ns and reliability higher than 99.999% for URLLCs.
Terminal densities of 1 million of terminals per square kilometer for massive IoT applications.
Per-user data-rate of the order of Terabit/s for broadband applications.”

Let’s break this down, bullet by bullet.

First bullet: In 1 ns, light travels 30 cm in free space. So “end-to-end” here would mean a distance of at most 10 cm, to leave some fraction of a nanosecond for encoding, transmission, and decoding. But what useful wireless service is there where transceivers are within at most 10 cm? Next, a packet loss rate of 10^-5 means that the spectral efficiency must be very low. Together with a latency constraint of 1 ns, ultrahigh bandwidths must be used, which, in turn, makes the design of circuitry and antenna arrays extremely challenging. At least the channel can be expected to be benign (line-of-sight).

Where does stochastic geometry come in? Assuming that these ultrashort links live in a network and not in isolation, interference will play a role. Let us consider a Poisson bipolar network with normalized link distance 1, a path loss exponent α and Rayleigh fading. What is the maximum density of links that can be supported that have an outage of at most ε? This quantity is known as the spatial outage capacity (SOC). For small ε, which is our regime of interest here, we have

$\displaystyle\text{SOC}\sim\left(\frac{\varepsilon}{\rho}\right)^\delta c_\delta,\quad \varepsilon\to 0,$

where δ=2/α and c_δ is a constant that only depends on the path loss exponent 2/δ. ρ is the spectral efficiency (in bits/s/Hz or bps/Hz). This shows the fundamental tradeoff between outage and spectral efficiency: Reducing the outage by a factor of 10 reduces the rate of transmission by the same factor if the same link density is to be maintained. Compared to a more standard outage constraint of 5%, this means that the rate must be reduced by a factor 5,000 to accommodate the 99.999% reliability requirement. Now, say we have 0.5 ns for the transmission of a message of 50 bits, the rate is 100 Gbps. Assuming a very generous spectral efficiency of 100 bps/Hz for a system operating at 5% outage, this means that 100 Gbps must be achieved at a spectral efficiency of a mere 0.02 bps/Hz. So we would need 5 THz of bandwidth to communicate a few dozen bits over 10 cm.
Even relaxing the latency constraint to 1 μs still requires 5 GHz of bandwidth.

In cellular networks, the outage-rate relationship is governed by a very similar tradeoff.
For any stationary point process of base stations and Rayleigh fading, the SIR meta distribution asymptotically has the form

$\displaystyle \bar F(\rho,\varepsilon)\sim\left(\frac{\varepsilon}{\rho}\right)^\delta C_\delta,\quad \varepsilon\to 0,$

where C_δ again depends only on the path loss exponent. This is the fraction of users who achieve a spectral efficiency of ρ with an outage less than ε, remarkably similar to the bipolar result. To keep this fraction fixed at, say, 95%, again the spectral efficiency needs to be reduced in proportion to a reduction of the outage constraint ε.

Second bullet: Per the classification and nomenclature in a dense debate, this density falls squarely in the tremendously dense class, above super-high density and extremely high density. So what do the anticipated 100 devices in an average home or 10,000 devices in an average parking lot do? What kind of messages are they exchanging or reporting to a hub? How often? What limits the performance? These devices are often said to be “connected“, without any specification what that means. Only once this is clarified, a discussion can ensue whether such tremendous densities are realistic.

Third bullet: Terabit-per-second (Tbps) rates require at least 10 GHz of spectrum, optimistically. 5G in its most ambitious configuration, ignoring interference, has a spectral efficiency of about 50 bps/Hz, and, barring any revolutionary breakthrough, more than 100 bps/Hz does not appear feasible in the next decade. Similarly, handling a signal 10 GHz wide would be an order of magnitude beyond what is currently possible. Plus such large junks of spectrum are not even available at 60 GHz (the current mm-wave bands). At 100 GHz and above, link distances are even more limited and more strongly subject to blockages, and analog beamforming circuitry becomes much more challenging and power-hungry. Most importantly, though, peak rates are hardly achieved in reality. In the 5G standard, the user experienced data rate (the rate of the 5-th percentile user) is a mere 1% of the peak rate, and this fraction has steadily decreased over the cellular generations:

So even if 1 Tbps peak rates became a reality, users would likely experience between 1 Gbps to at most 10 Gbps – assuming their location is covered, which may vary over short spatial scales. Such user percentile performance can be analyzed using meta distributions.

In conclusion, while setting ambitious goals may trigger technological advances, it is important to be realistic of what is achievable and what performance the user actually experiences. For example, instead of focusing on 1 Tbps peak rates, we could focus on delivering 1 Gbps to 95% of the users, which may still be very challenging but probably achievable and more rewarding to the user. And speaking of billions of “connected devices” is just marketing unless it is clearly defined what being connected means.

For more information on the two analytical results above, please see this paper (Corollary 1) and this paper (Theorem 3).

What to expect (over)

In performance analyses of wireless networks, we frequently encounter expectations of the form

$\displaystyle\mathbb{E}\log(1+{\rm SIR}),\qquad\qquad\qquad\qquad\qquad\qquad (*)$

called average (ergodic) spectral efficiency (SE) or mean normalized rate or similar, in units of nats/s/Hz. For networks models with uncertainty, its evaluation requires the use stochastic geometry. Sometimes the metric is also normalized per area and called area spectral efficiency. The SIR is expressed in the form

$\displaystyle {\rm SIR}=\frac{h_y \|y\|^{-\alpha}}{\sum_{x\in\Phi} h_x \|x\|^{-\alpha}},$

with Φ being the point process of interferers.
There are several underlying assumption made when claiming that (*) is a relevant metric:

It is assumed that codewords are long enough and arranged in a way (interspersed in time, frequency, or across antennas) such that fading is effectively averaged out. This is reasonable for several current networks.
It is assumed that desired signal and interference amplitudes are Gaussian. This is sensible since if a decoder is intended for Gaussian interference, then the SE is as if the interference amplitude were indeed Gaussian, regardless of its actual distribution.
Most importantly and questionably, taking the expectation over all fading random variables h_x implies that the receiver has knowledge of all of them. Gifting the receiver with all the information of the channels from all interferers is unrealistic and thus, not surprisingly, leads to (*) being a loose upper bound on what is actually achievable.

So what is a more realistic and accurate approach? It turns out that if the fading in the interferers’ channels is ignored, i.e., by considering

$\displaystyle {\rm SIR}^\prime=\frac{h_y \|y\|^{-\alpha}}{\sum_{x\in\Phi} \|x\|^{-\alpha}},$

we can obtain a tight lower bound on the SE instead of a loose upper bound. A second key advantage is that this formulation permits a separation of temporal and spatial scales, in the sense of the meta distribution. We can write

$\displaystyle {\rm SIR}^\prime=h_y\rho,\qquad\text{where }\; \rho=\frac{\|y\|^{-\alpha}}{\sum_{x\in\Phi} \|x\|^{-\alpha}}$

is a purely geometric quantity that is fixed over time and cleanly separated from the time-varying fading term h_y. Averaging locally (over the fading), the SE follows as

$\displaystyle C(\rho)=\mathbb{E}_h \log(1+h\rho),$

which is a function of (conditioned on) the point process. For instance, with Rayleigh fading,

$\displaystyle C(\rho)=e^{1/\rho} {\rm Ei}_1(1/\rho),$

where Ei₁ is an exponential integral. The next step is to find the distribution of ρ to calculate the spatial distribution of the SE – which would not be possible from (*) since it is an “overall average” that lumps all randomness together. In the case of Poisson cellular networks with nearest-base station association and path loss exponent 2/δ, a good approximation is

Here s* is given by

$\displaystyle s^{*\delta}\gamma(-\delta,s^*)=0,$

and γ is the lower incomplete gamma function. This approach lends itself to extensions to MIMO. It turns out that the resulting distribution of the SE is approximately lognormal, as illustrated in Fig. 1.

Figure 1: Spatial distribution of ergodic spectral efficiency for 2×2 MIMO in a Poisson cellular network and its lognormal approximation (red).

For SISO and δ=1/2 (a path loss exponent of 4), this (approximative) analysis shows that the SE achieved in 99% of the network is 0.22 bits/s/Hz, while a (tedious) simulation gives 0.24 bits/s/Hz. Generally, for small ξ, 1/ln(1/ξ) is achieved by a fraction 1-ξ of the network. As expected from the discussion above, this is a good lower bound.

In contrast, using the SIR distribution directly (and disregarding the separation of temporal and spatial scales), from

$\displaystyle \bar F_{\rm SIR}(\theta)=0.99 \quad\Longrightarrow\quad \theta=-20\text{ dB},$

we would obtain an SE of only log₂(1.01)=0.014 bits/s/Hz for 99% “coverage”, which is off by a factor of 16! So it is important that coverage be gleaned from the ergodic SE rather than a quantity subject to the small-scale variations of fading. See also this post.

The take-aways for the ergodic spectral efficiency are:

Avoid mixing time and spatial scales by expecting first over the fading and separately over the point process; this way, the spatial distribution of the SE can be obtained, instead of merely its average.
Avoid gifting the receiver with information it cannot possibly have; this way, tight lower bounds can be obtained instead of loose upper bounds.

The details can be found here.

Signal-to-interference, reversed

Interference is the key performance-limiting factor in wireless networks. Due to the many unknown parts in a large network (transceiver locations, activity patterns, transmit power levels, fading), it is naturally modeled as a random variable, and the (only) theoretical tool to characterize its distribution is stochastic geometry. Accordingly, many stochastic geometry-based works focus on interference characterization, and some closed-form expressions have been obtained in the Poisson case.

If the path loss law exhibits a singularity at 0, such as the popular power-law r^-α, the interference (power) may not have a finite mean if an interferer can be arbitrarily close to the receiver. For instance, if the interferers form an arbitrary stationary point process, the mean interference (at an arbitrary fixed location) is infinite irrespective of the path loss exponent. If α≤2, the interference is infinite in an almost sure sense.

This triggered questions about the validity of the singular path loss law and prompted some to argue that a bounded (capped) path loss law should be used, with α>2, to avoid such divergence of the mean. Of course the singular path loss law becomes unrealistic at some small distance, but is it really necessary to use a more complicated model that introduces a characteristic distance and destroys the elegant scale-free property of the singular (homogeneous) law?

The relevant question is to which extent the performance characterization of the wireless network suffers when using the singular model.

First, for practical densities, there are very few realizations where an interferer is within the near-field, and if it is, the link will be in outage irrespective of whether a bounded or singular model is used. This is because the performance is determined by the SIR, where the interference is in the denominator. Hence whether the interference is merely large or almost infinite makes no difference – for any reasonable threshold, the SIR will be too small for communication.
Second, there is nothing wrong with a distribution with infinite mean. While standard undergraduate and graduate-level courses rarely discuss such distributions, they are quite natural to handle and pose no significant extra difficulty.

That said, there is a quantity that is very useful when it has a finite mean: the interference-to-(average)-signal ratio ISR, defined as

$\displaystyle {\rm ISR}=\frac{\sum_{x\in\Phi\setminus\{x_0\}} h_x \|x\|^{-\alpha}}{\|x_0\|^{-\alpha}},$

where x₀ is the desired transmitter and the other points of Φ are interferers. The h_x are the fading random variables (assumed to have mean 1), only present in the numerator (interference), since the signal power here is averaged over the fading.
Taking the expectation of the ISR eliminates the fading, and we arrive at the mean ISR

$\displaystyle {\rm MISR}=\mathbb{E} \sum_{x\in\Phi\setminus\{x_0\}}\left(\frac{\|x_0\|}{\|x\|}\right)^{\alpha},$

which only depends on the network geometry. It follows that the SIR distribution is

$\displaystyle \mathbb{P}({\rm SIR}<\theta)=\mathbb{P}(h<\theta\, {\rm ISR})=\mathbb{E} F_h(\theta\,{\rm ISR}),$

where h is a generic fading random variable. If h is exponential (Rayleigh fading) and the MISR is finite,

$\displaystyle F_h(x)\sim x\qquad\Longrightarrow\qquad \mathbb{P}({\rm SIR}<\theta)\sim \theta\,{\rm MISR}.$

Hence for small θ, the outage probability is proportional to θ with proportionality factor MISR. This simple fact becomes powerful in conjunction with the observation that in cellular networks, the SIR distributions (in dB) are essentially just shifted versions of the basic SIR distribution of the PPP (and of each other).

Figure 1: Examples for SIR distributions in cellular networks that are essentially shifted versions of each other.

In Fig. 1, the blue curve is the standard SIR ccdf of the Poisson cellular network, the red one is that of the triangular lattice, which has the same shape but shifted by about 3 dB, with very little dependence on the path loss exponent. The other two curves may be obtained using base station silencing and cooperation, for instance. Since the shift is almost constant, it can be determined by calculating the ratios of the MISRs of the different deployments or schemes. The asymptotic gain relative to the standard Poisson network (as θ→0) is

$\displaystyle G_0=\frac{\rm MISR_{PPP}}{{\rm MISR}},\quad \text{where }\; {\rm MISR_{PPP}}=\frac{2}{\alpha-2},\quad \alpha>2,$

The MISR in this expression is the MISR for an alternative deployment or architecture. The MISR for the PPP is not hard to calculate. Extrapolating to the entire distribution by applying the gain everywhere, we have

$\displaystyle \bar F_{\rm SIR}(\theta) \approx \bar F_{\rm SIR}^{\rm PPP}(\theta/G_0).$

This approach of shifting a baseline SIR distribution was proposed here and here. It is surprisingly accurate (as long as the diversity order of the transmission scheme is unchanged), and it can be extended to other types of fading. Details can be found here.

Hence there are good reasons to focus on the reversed SIR, i.e., the ISR.

Path loss point processes

Naturally the locations of wireless transceivers are modeled as a point process on the plane or perhaps in the three-dimensional space. However, key quantities that determine the performance of a network do not directly nor exclusively depend on the locations but on the received powers. For instance, a typical SIR expression (at the origin) looks like

$\displaystyle {\rm SIR}=\frac{P_y h_y \|y\|^{-\alpha}}{\sum_{x\in\Phi} P_x h_x \|x\|^{-\alpha}},$

where y is the location of the intended transmitter and Φ is the point process of interferers. P_x and h_x are the transmit powers and fading coefficients of x, respectively. It is apparent that what matters are the distances raised to some power, not the locations themselves. So instead of working with Φ⊂ℝ², we can focus on the one-dimensional process

$\displaystyle \Psi\triangleq\{x\in\Phi\colon \|x\|^{\alpha}/h_x\},$

called the path loss point process (PLPP) (with fading). The reason why the positive exponent α is preferred over -α is that otherwise the resulting point process is no longer locally finite (assuming Φ is stationary) since infinitely many points would fall in the interval [0,ε] for any ε>0. Transmit power levels could be included as displacements, either deterministically or randomly.

Path loss processes are particularly useful when Φ is a PPP. By the mapping and displacement theorems, the PLPPs are also PPPs whose intensity function is easy to calculate. For a stationary PPP Φ of intensity λ and iid fading, the intensity function of Ψ is

$\displaystyle \mu(r)=\pi\lambda\delta r^{\delta-1}\mathbb{E}(h^\delta),\quad r\geq 0, \delta\triangleq2/\alpha.$

where h is a generic fading random variable. If h has mean 1, then for δ<1, which is necessary to keep the interference finite, 𝔼(h^δ)<1 from Jensen’s inequality, hence the effect of fading is a reduction of the intensity function by a fixed factor.

As an immediate application we observe that fading reduces the expected number of connected nodes, defined as those whose received power is above a certain threshold, by the δ-th moment of the fading coefficients.

More importantly, PLPPs lead to two key insights for Poisson cellular networks. Let us assume the elements of Ψ are ordered and denoted as ξ₁<ξ₂<… . Then the SIR with instantaneously-strongest base station association (ISBA) is

$\displaystyle {\rm SIR}=\frac{\xi_1^{-1}}{\sum_{i=2}^\infty \xi_i^{-1}}.$

First, it is not hard to show that for ISBA with Rayleigh fading, the SIR distribution does not depend on the density of the underlying PPP. But since the effect of fading is but a scaling of the density, it follows that the SIR distribution does not depend on the fading statistics, either. In particular, the result for Rayleigh fading also applies to the non-fading case (where ISBA corresponds to nearest-base station association, NBA), which is often hard to analyze in stochastic geometry models.

Second, the intensity function of the PLPP also shows that the SIR performance of the heterogeneous independent Poisson (HIP) model is the same as that of the simple PPP model. The HIP model consists of an arbitrary number n of tiers of base stations, each modeled as an independent PPP of arbitrary densities λ_k and transmitting at arbitrary (deterministic) power levels P_k. The point process of inverse received powers (i.e., the PLPP with transmit powers included) from tier k has intensity

$\displaystyle \mu_k(r)=\pi\lambda_k\delta r^{\delta-1}\mathbb{E}(h^\delta)P_k^\delta,\quad r\geq 0.$

Since the superposition of n PPPs is again a PPP, the overall intensity is just the sum of the μ_k, which is still proportional to r^δ-1. This shows that the SIR performance (with ISBA or NBA) of any HIP model is the same as that of just a single PPP.

For further reading, please refer to A Geometric Interpretation of Fading in Wireless Networks: Theory and Applications and The Performance of Successive Interference Cancellation in Random Wireless Networks.

The transdimensional approach

In vehicular networks, transceivers are inherently confined to a subset of the two-dimensional Euclidean space. This subset is the street system where cars are allowed to move. Accordingly, stochastic geometry models for vehicular networks usually consist of two components: A set of streets and a set of point processes, one for each street, representing the vehicles. The most popular model is the Poisson line process (PLP) for the streets, combined with one-dimensional PPPs of vehicles on each line (street).

This PLP-PPP model does not have T-junctions, only intersections. Accordingly, all vehicles are of order 2 or 4, per the taxonomy introduced here. The order is determined by the number of directions in which a vehicle can move.

The PLP-PPP is a Cox process due to the independent one-dim. PPPs, and the underlying street system determining the intensity measure (the line process) is also based on the PPP. Consequently, the PLP-PPP inherits a certain level of tractability from the PPP, in the sense that exact expressions can be derived for some quantities of interest. In particular, the SIR distribution (complementary cumulative distribution function, ccdf) at the typical vehicle for a transmitter at a fixed distance can be derived without difficulty. However, the expression requires the evaluation of two nested improper integrals. While such a result certainly has its value, it does not give direct insight how the resulting SIR distribution depends on the network parameters. Also, other metrics that depend on the SIR often require further integration, most importantly the SIR meta distribution, which is calculated from the higher moments of the conditional SIR ccdf (given the point process).

This raises the question whether it is possible to find a closed-form result that is much more quickly evaluated and provides a tight approximation. Simply replacing the PLP-PPP by a two-dimensional PPP produces poor results, especially in the high-reliability regime (where the SIR ccdf is near 1). Similarly, considering only the one street that the typical vehicle lies on (i.e., using only a one-dimensional PPP) ignores all the interference from the vehicles on the other streets, which strongly affects the tail of the distribution.

How about a combination of the two – a superposition of a one-dimensional PPP for the typical vehicle’s street and a two-dimensional PPP for the other vehicles? In this approach, PPPs of two different dimensions are combined to a transdimensional PPP (TPPP). It accurately characterizes the interference from nearby vehicles, which are likely to lie on the same street as the typical vehicle, and captures the remaining interference without the complexity of the PLP. The three key advantages of this approach are:

The TPPP leads to closed-form results for the SIR ccdf that are asymptotically exact, both in the lower and upper tails (near 0 and near infinity).
The results are highly accurate over the entire range of the SIR ccdf, and they are obtained about 100,000 times faster than the exact results. Hence, if fast evaluation is key and a time limit of, say, one μs is specified, the transdimensional approach yields more accurate results than the exact expression. Put differently, the exact expression only leads to higher accuracy if ample computation time is available.
The simplicity of the TPPP extends to all moments of the conditional success probability, which greatly simplifies the calculation of the SIR meta distribution.

The TPPP approach is also applicable to other street systems, including the Poisson stick model (where streets are modeled as line segments of random length) and the Poisson lilypond model, which forms T-junctions (where vehicles are of order 3). For the stick model with independent lengths, the exact expression of the nearest-neighbor distance distribution involves six nested integrals, hence a transdimensional is certainly warranted. More details can be found here.